I don't have a degree in computer science, and it's okay if you don't either! Lots of us Rubyists don't have formal computer science credentials. So for a long time, I avoided learning about big-O notation. It looks a little too much like higher math. I mean just look at something like: O(N^2). Come on!
Instead, I learned a few useful rules of thumb for thinking about scalability:
- Finding a specific item in a Hash is faster than finding an item in a similarly sized Array
- Avoid nested loops
- Watch out for accidental database queries when generating lists in your views
These rules are pretty useful, but unless you understand WHY they work, you're going to find yourself making mistakes and having inexplicable performance problems. Big-O notation doesn't have to be scary. Once you understand some basic principles, you'll find it to be a straightforward way of thinking about how certain chunks of code scale.
Even if you don't think you'll use big-O notation in your day-to-day work, you'll likely encounter it in a coding interview at some point in your career. Dig in with us as we demystify a bit of the complexity.
What is big-O notation?
Big-O notation is a fancy way of describing how your code's performance depends on how much data it processes. It's a way to quickly explain, or "notate" how a chunk of code's execution time (or memory) grows as its input grows. If you're writing a function that takes an array, it's wise to know how the size of the array affects the code that processes it. It might not matter when the array size is small, but time or space complexity can become a problem as it grows.
Big-O measures more than one thing
When it comes to big-O notation for complexity, performance means one of two things: speed or RAM usage. In computer science class, you'd refer to these as "time complexity" and "space complexity." Big-O notation relates to both, but we'll focus on time complexity (rather than space complexity, which represents how much memory is needed) here since it's the most common concern. You'll otherwise often see this metric referred to as "time and space complexity".
You would expect that processing an array of 100 items would be slower than an array of 10 items. But by how much? Ten times as much? One hundred times as much? What about one thousand times as much?
It's not a big deal with small datasets, but if your app gets exponentially slower for each row in the database it soon becomes a problem.
Before we get into the details, I made a quick chart showing common big-Os with emoji showing how they'll make you feel as your data scales.
| Big O | Rank | Meaning |
|---|---|---|
| O(1) | 😎 | Speed doesn't depend on the size of the dataset |
| O(log n) | 😁 | 10x the data means 2x more time |
| O(n) | 😕 | 10x the data means 10x more time |
| O(n log n) | 😖 | 10x the data means about 20x more time |
| O(n^2) | 😫 | 10x the data take 100x more time |
| O(2^n) | 😱 | The dilithium crystals are breaking up! |
So when someone says Array#bsearch is better than Array#find because it's O(log n) vs O(n) you can just compare 😁 to 😕 and see that they might be onto something. These emojis can serve as an easier reference than mathematical notation It's certainly "more efficient" to grow logarithmically than linearly.
For something a little more robust, check out the Big-O cheat sheet below:

Big-O is only concerned with asymptotic complexity
One relatively important concept about big-O notation is that it's really only concerned with asymptotic growth.
What the heck is "asymptotic"?
Let's travel back to high school algebra, dust off our textbook, and open it to the chapters on limits and asymptotes.
- Limit analysis: seeing what happens to a function as it approaches some value
- Asymptotic analysis: seeing what happens as f(x) approaches infinity
For example, let's say we plot the function f(x) = x^2 + 4x.
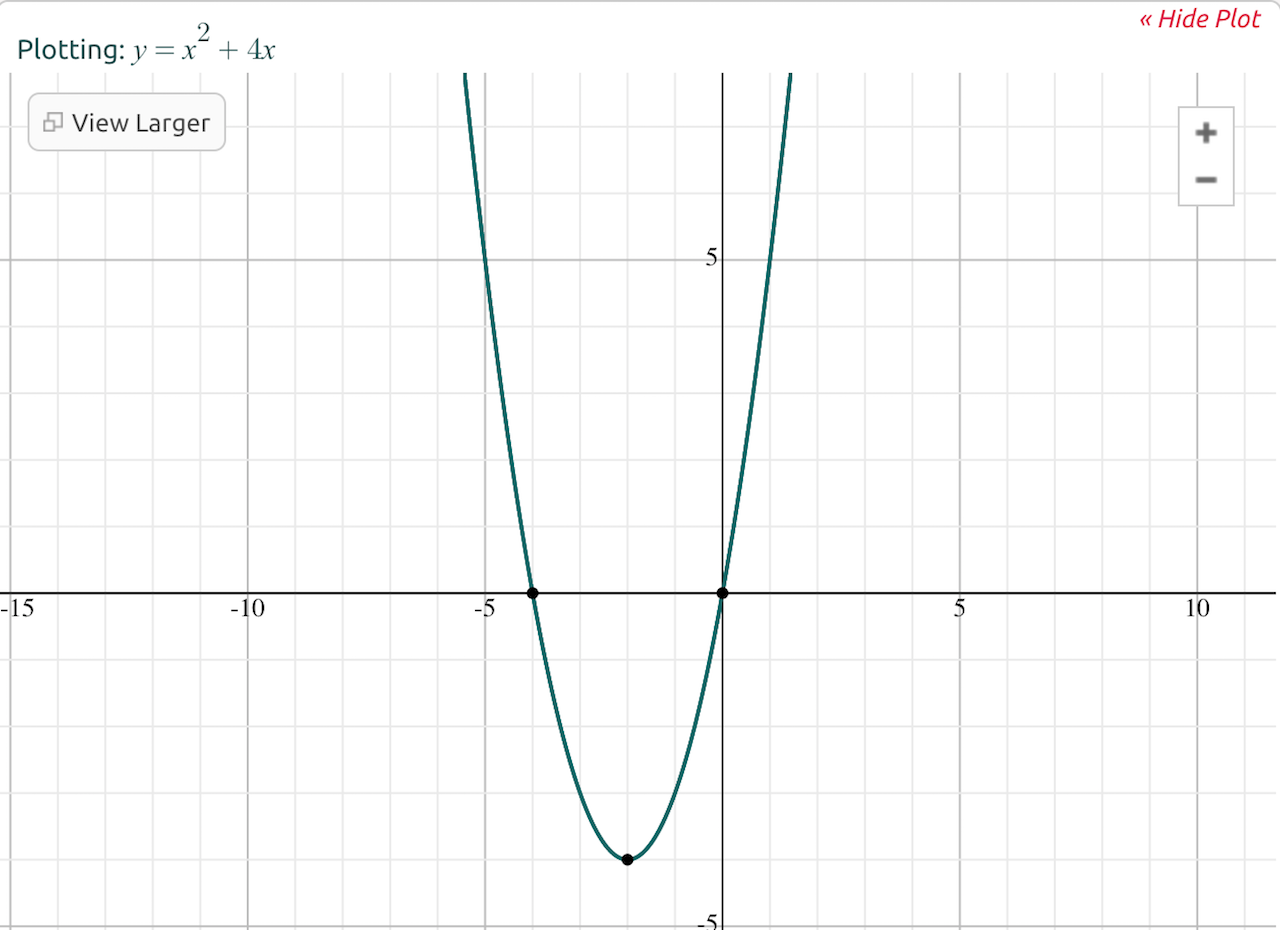
We can perform the following analyses:
- Limit analysis: As x increases, f(x) approaches infinity, so we can say that the limit of f(x) = x^2 + 4x as x approaches infinity is infinity.
- Asymptotic analysis: As x becomes very large, the 4x term becomes insignificant compared to the x^2 term. So, we can say that f(x) = x^2 + 4x becomes almost equivalent to f(x) = x^2 for values of x approaching infinity.
To understand how we can say that part of a function becomes "insignificant," consider what happens when you plug different numbers into the original function. For example, when x = 1, the function returns 1 + 4 (which equals 5). However, when x = 2,000, the function returns 4,000,000 + 8,000 (which equals 4,008,000) -- the x^2 term contributes much more to the total than the 4x.
How do asymptotes apply to big-O notation?
If I ask you how long it will take to find a needle in a haystack, you will want to know how much hay is in the stack. If I respond "10 pieces," I bet you will be pretty confident you can find the needle within a minute or two, but if I say "1,000 pieces," you probably won't be as excited.
There's one other piece of information you should know. How much longer does it take to search the stack for each piece of hay added? And what happens as the amount of hay approaches infinity?
Deciphering big-O notation
You don't have to memorize all the different big-O values if you understand how the notation works. Sure, it helps a bit to understand some math as you can intuitively have an idea of what each notation means, but seeing the notations often enough has a close enough effect.
Take, for example, the horrible horrible O(2^n) time complexity. If we were to express that in Ruby, it might look like this:
# O(2^n) translated to Ruby
def o(n)
2 ** n # This is ruby for 2^n
end
Still not obvious? How about if I rename the method and argument to something more user-friendly?
# O(2^n) translated to prettier Ruby
def execution_time(size_of_dataset)
2 ** size_of_dataset
end
You can do this for all of them:
# O(1)
def o1_execution_time(size_of_dataset)
1
end
# O(n)
def on_execution_time(size_of_dataset)
size_of_dataset
end
# O(n^2)
def on2_execution_time(size_of_dataset)
size_of_dataset * size_of_dataset
end
...etc
Now that you know how the notation works, let's take a look at some typical ruby code and see how it relates.
O(1) - Constant time complexity
When we say that something is O(1) time complexity it means that its speed doesn't depend on the size of its data set. For example, hash lookup times don't depend on the hash size, which makes it one of my favorite data structures:
# These should all take the same amount of time
hash_with_100_items[:a]
hash_with_1000_items[:a]
hash_with_10000_items[:a]
This is why we tend to say that hashes are faster than arrays for larger datasets, and it's why it's important to have a baseline understanding of data structures. This is the best-case scenario for big-O complexity. It means that you can infinitely scale the input size and the execution time will stay the same!
O(n) - Linear time complexity
In contrast, Array#find is O(n) time complexity. That means Array#find depends linearly on the number of items in the array. An array with 100 items will take 100 times longer to search than an array with one item.
A lot of code that iterates over arrays follows the O(n) pattern.
(0..9).each do |i|
puts i
end
# This example is 1/2 the speed of the previous one because it contains 2x the items.
(0..19).each do |i|
puts i
end
What does a function that runs in linear time look like?
The first example that comes to mind of a programming solution that runs in linear time complexity is a linear search. Let's do a big-O analysis of the linear search algorithm. A linear search starts at the beginning of a dataset and traverses until the target element is found.
Here is an implementation in Ruby:
def find_number_via_linear_search(array, target)
counter = 0
# iterate through the given array starting
# at index 0 and continuing until the end
while counter < array.length
if array[counter] == target
# exit if target element found
return "linear search took: #{counter} iterations"
else
counter += 1
end
end
return "#{target} not found"
end
To make the output a little more interesting and useful, we could give this method a spin like this:
# Let's create an array with 50 integers
# and then re-arrange the order to make
# things more interesting
array = [*1..50].shuffle
find_number_via_linear_search(array, 24)
I ran this a few times and got the following results:
=> "linear search took: 10 iterations"
=> "linear search took: 11 iterations"
=> "linear search took: 26 iterations"
When analyzing the big-O time complexity of a function, we mostly care about the worst-case scenario (a.k.a. the upper asymptotic bound).
Thinking about this intuitively, the smallest number of iterations would be 1. That occurs when the target element is in position 0 in the array. The largest number of iterations (or worst-case scenario) would be 50. This will happen when the target element is not found in the array.
If our array has 100 elements, the worst-case will be 100 iterations. 200 elements? 200 iterations. Thus, the big-O notation for linear search is simply O(n), where n is the number of elements.
O(n^2) - Exponential time complexity
Code that fits an O(n^2) profile tends to involve nested loops. That makes sense if you think about it. One loop gives you O(n), a second nested loop gives you O(n^2). If for some unholy reason, you had a 5-level nested loop, it'd be O(n^5).
data = (0..100)
data.each do |d1|
data.each do |d2|
puts "#{ d1 }, #{ d2 }"
end
end
This explains why nested loops are so inefficient, and it's a perfect example of how having a good understanding of big-O complexity gives you an edge. As you evaluate more and more functions for their complexity, you'll find more and more common patterns like nested loops.
O(log n) - Logarithmic complexity
Let's consider binary search next. Here's how you do a binary search of a pre-sorted array:
- Take the middle element
- If
element == targetwe're done - If
element > targetdiscard the top half of the array - If
element < targetdiscard the bottom half of the array - Start over at step 1 with the remaining array
Note: If you're a Rubyist, there is a built-in b-search method that implements this algorithm for you!
For example, let's say that you have a dictionary and you're looking for the word "pineapple." We'd go to the middle page of the dictionary. If it happened to have the word "pineapple," we'd be done!
But my guess is the middle of the dictionary wouldn't be in the "p's" yet, so maybe we'd find the word "llama." The letter "L" comes before "P," so we would discard the entire lower half of the dictionary. Next, we'd repeat the process with what remained.
As with linear search, the best-case run time for a binary search is one iteration. But what's the worst case? Here is an example array that has 16 elements -- let's pretend that we want to use a binary search to find the number 23:
[2, 3, 15, 18, 22, 23, 24, 50, 65, 66, 88, 90, 92, 95, 100, 200]
The first step would be to look at the number at index 7, which is 50. Since 50 is greater than 23, we discard everything to the right. Now our array looks like this:
[2, 3, 15, 18, 22, 23, 24, 50]
The middle element is now 18, which is less than 23, so we discard the lower half this time:
[22, 23, 24, 50]
Which becomes:
[22, 23]
You can probably see where this is going! It finally becomes:
[23]
In total, we had to divide the array by 4 times to find the number we were targeting in the array, which had a length of 16.
To generalize this, the worst-case scenario for binary search is equal to the maximum number of times we can divide the array in half.
O(n log n) - Loglinear complexity
O(n log n) code is often the result of someone finding a clever way to reduce the amount of work that an otherwise O(n^2) algorithm would do.
You wouldn't be able to just look at a piece of code and tell it's O(n log n). This is where the higher math comes in, and it's also where I bow out.
But it is important to know about O(n log n) because it describes a lot of common search algorithms. Ruby's Array#sort uses the venerable quicksort algorithm, which on average is O(n log n) and worst-case is O(n^2)
If you're not familiar with quicksort, check out this excellent demonstration.
Putting it all together: How it affects your database
One of the most common problems with new web applications is that they're fast on the developer's computer, but in production, they get slower and slower.
This happens because the amount of records in your database grows over time, but your code is asking the DB to do operations that don't scale well. ie. O(n) or worse.
For example, did you know that in Postgres, count queries are always O(n)?
# This makes the DB iterate over every row of Users
# ...unless you're using a Rails counter cache.
Users.count
We can see this by using the Postgres explain command. Below, I use it to get the query plan for a count query. As you can see, it plans on doing a sequential scan (that means looping) over all 104,791 rows in the table.
# explain select count(*) from users;
QUERY PLAN
-----------------------------------------------------------------
Aggregate (cost=6920.89..6920.90 rows=1 width=0)
-> Seq Scan on users (cost=0.00..6660.71 rows=104701 width=0)
(2 rows)
Lots of common rails idioms can trigger unintentional sequential scans unless you specifically optimize the database to prevent them.
# This asks the DB to sort the entire `products` table
Products.order("price desc").limit(1)
# If `hobby` isn't indexed, the DB loops through each row of Users to find it.
User.where(hobby: "fishing")
You can use the explain command to see that as well. Here we see we're doing a sort (probably quicksort) on the whole table. If there are memory constraints, it may have chosen a different sorting algorithm with different performance characteristics.
# explain select * from users order by nickname desc limit 1;
QUERY PLAN
-------------------------------------------------------------------------
Limit (cost=7190.07..7190.07 rows=1 width=812)
-> Sort (cost=7190.07..7405.24 rows=104701 width=812)
Sort Key: nickname
-> Seq Scan on users (cost=0.00..6606.71 rows=104701 width=812)
The answer to all these problems is, of course, indexing. Telling the database to use an index is a little like in Ruby when you use a hash lookup O(1) instead of an array find O(n).
Applying your knowledge of big-O notation
I hope this has been a useful introduction to big-O notation and how it impacts you as a Ruby developer! Taking the time to wrap your head around how your code scales as its inputs grow is an important piece of writing code, even if it's for simple Rails apps.
Any time you can find ways to get code that runs in exponential time to run in linear time, your users and infrastructure team will thank you. If you enjoyed this article, consider singing up for the Honeybadger newsletter to get more like this in your inbox. Happy coding!


